دستگاه معادلات (مرحله اول سی و یکمین المپیاد ریاضی- سوال 6):

چند زوج مرتب (x , y) از اعداد حقیقی، در دستگاه معادلات زیر صدق می کند؟

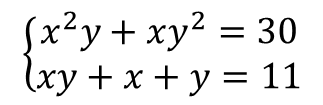
پاسخ: 4 عدد (طبیعی)

یک راه آسان برای حل معادلات این است که اول از اعداد صحیح استفاده کنیم.

با تبدیل دستگاه معادلات به صورت زیر داریم:

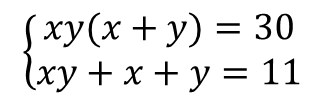
اول با در نظر گرفتن اعداد طبیعی می فهمیم که xy (x + y) = 30 حاصلضرب دو عدد است.

حال حالاتی را در نظر می گیریم که اعداد طبیعی از حاصلضرب دو عدد برابر 30 شوند:

1 × 30 = 30

2 × 15 = 30

3 × 10 = 30

5 × 6 = 30

6 × 5 = 30

10 × 3 = 30

15 × 2 = 30

30 × 1 = 30

حال باید یکی از اعداد حاصلضرب را برابر xy و دیگری را برابر x + y گذاریم و امتحان کنیم.

در سه حالت اول و آخر امکان ندارد دو عدد طبیعی x و y در معادله جواب دهند. اما در دو حالت میانی به این صورت داریم:

5 × 6 = 30 --> {x, y € N |xy = 6, x + y =5, (x, y = 2, 3)}

--> * x = 2, y = 3                     * x = 3, y = 2

6 × 5 = 30 --> {x, y € N |xy = 5, x + y =6, (x, y = 1, 5)}

--> * x = 1, y = 5                     * x = 5, y = 1

این کار را با اعداد صحیح و در آخر با اعداد حقیقی انجام باید داد. (حتما انجام می دهیم تا مسئله را اشتباه حل نکنیم. اگر چه فقط وقت ما را می گیرد.)